无穷级数
基本概念

级数的基本性质
线性性质:
若 $\sum_{n=1}^{\infty}u_n$ 与 $\sum_{n=1}^{\infty}v_n$ 分别收敛于 S 和 $\sigma$ , 则 $\sum_{n=1}^{\infty}(ku_n+\lambda v_n)$ 也收敛 , 且其和为$kS+\lambda \sigma$ , 其中 $k$ , $\lambda$为常数
有限项性
在级数中去掉、加上或者改变有限项,不会改变级数的收敛性
加括号性
收敛级数加括号后形成的级数, 仍收敛于原级数的和; 但加括号后所形成的级数收敛, 去括号后原来的级数未必收敛
情况一:收敛级数加括号后形成的级数,仍收敛于原级数的和
原级数: 交错调和级数 $\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \dots$
这个级数根据莱布尼茨判别法是收敛的,它的和是 $\ln 2$。
加括号后形成的级数: 我们将相邻的两项加括号: $\left(1 - \frac{1}{2}\right) + \left(\frac{1}{3} - \frac{1}{4}\right) + \left(\frac{1}{5} - \frac{1}{6}\right) + \dots$
这个级数可以写成 $\sum_{k=1}^{\infty} \left(\frac{1}{2k-1} - \frac{1}{2k}\right)$。
每一项化简后为 $\frac{2k - (2k-1)}{(2k-1)(2k)} = \frac{1}{(2k-1)(2k)}$。
所以,加括号后的级数是 $\sum_{k=1}^{\infty} \frac{1}{(2k-1)(2k)} = \frac{1}{1 \cdot 2} + \frac{1}{3 \cdot 4} + \frac{1}{5 \cdot 6} + \dots$
结果: 这个加括号后的级数仍然收敛。事实上,它的部分和序列是原级数部分和序列的子序列(只取了偶数项的部分和 $S_2, S_4, S_6, \dots$)。 由于原级数收敛,其部分和序列的极限是存在的,那么其任何子序列的极限也必然存在且等于原极限。 因此,加括号后的级数也收敛,并且它的和仍然是 $\ln 2$。
情况二:加括号后所形成的级数收敛,去括号后原来的级数未必收敛
原级数(发散): $\sum_{n=1}^{\infty} (-1)^{n-1} = 1 - 1 + 1 - 1 + 1 - 1 + \dots$
分析原级数: 加括号后形成的级数(收敛): 我们将相邻的两项加括号: $(1 - 1) + (1 - 1) + (1 - 1) + \dots$
这个级数可以写成 $\sum_{k=1}^{\infty} 0$。
加括号后的级数是 $0 + 0 + 0 + \dots$,这个级数显然是收敛的,它的和为 $0$。
必要条件
若 $\sum_{n=1}^{\infty}u_n$ 收敛 , 则 $\lim_{x \to \infty} u_n = 0$ , 其逆命题不成立 ; 但若 $\lim_{x \to \infty} u_n \neq 0$ , 那么$\sum_{n=1}^{\infty}u_n$ 一定发散.
比如调和级数
专题练习
用定义判别级数是否收敛
例题 : 用定义判别级数 $\sum_{n=1}^{\infty}\frac{1}{n(n+1)(n=2)}$ 是否收敛
求级数的和
例题: $\sum_{n=0}^\infty \frac{(\ln 3) ^n}{2}$
常用: 采用等比数列求和公式

利用级数的性质判别级数的敛散性

常数项级数的审敛法
正项级数

交错级数

任意项级数

三个重要 级数
- 调和级数: $\sum_{n=1}^{\infty}\frac{1}{n} = 1+\frac 1 2 + \frac 1 3 + \ldots + \frac 1 n + \ldots$ , 该级数发散
- 几何级数(等比级数) : $\sum_{n=1}^{\infty}aq^{n-1} = a+aq+aq^2 +\ldots +aq^{n-1} + \ldots$
- 当 $|q| < 1$ 时,级数收敛
- 当 $|q| \ge 1$ 时, 级数发散
- p级数: $\sum_{n=1}^{\infty}\frac{1}{n^p} = 1+\frac{1}{2^p}+\frac{1}{3^p}+\ldots + \frac{1}{n^p} + \ldots$
- 当 p>1 时 , 级数收敛
- 当 $p \le 1$ 时,级数发散
幂级数也是重点, 篇幅限制, 大家自行复习吧
【微分方程】基本概念

常见习题
求给定的原始式(函数族)所满足的微分方程
一般而言,包含个独立的任意常数的原始式,可产生不含任意常数的n阶微分方程,这个n阶方程式可以从+1个方醒中消去n个常数得到,而此 n+1 个方程是由原始式与将原始式对自变量微分n次所得到的n个方程组成
例一: 求给定的原始式所满足的微分方程:$y=A\cos{\alpha x}+B\sin{\alpha x}$ , A ,B 为任意常数, $\alpha$ 为一固定常数.

验证所给函数是相应微分方程的通解或解
例题: 验证 $y = x +C_1 e^x$ 是方程 $(x-y+1)y' = 1$ 的解

化积分方程为微分方程
例题: 判断 $y= x(\int{\frac{e^x}{x}},dx + C)$ (C为任意常数) 是否为方程 $xy' - y = xe^x$ 的通解
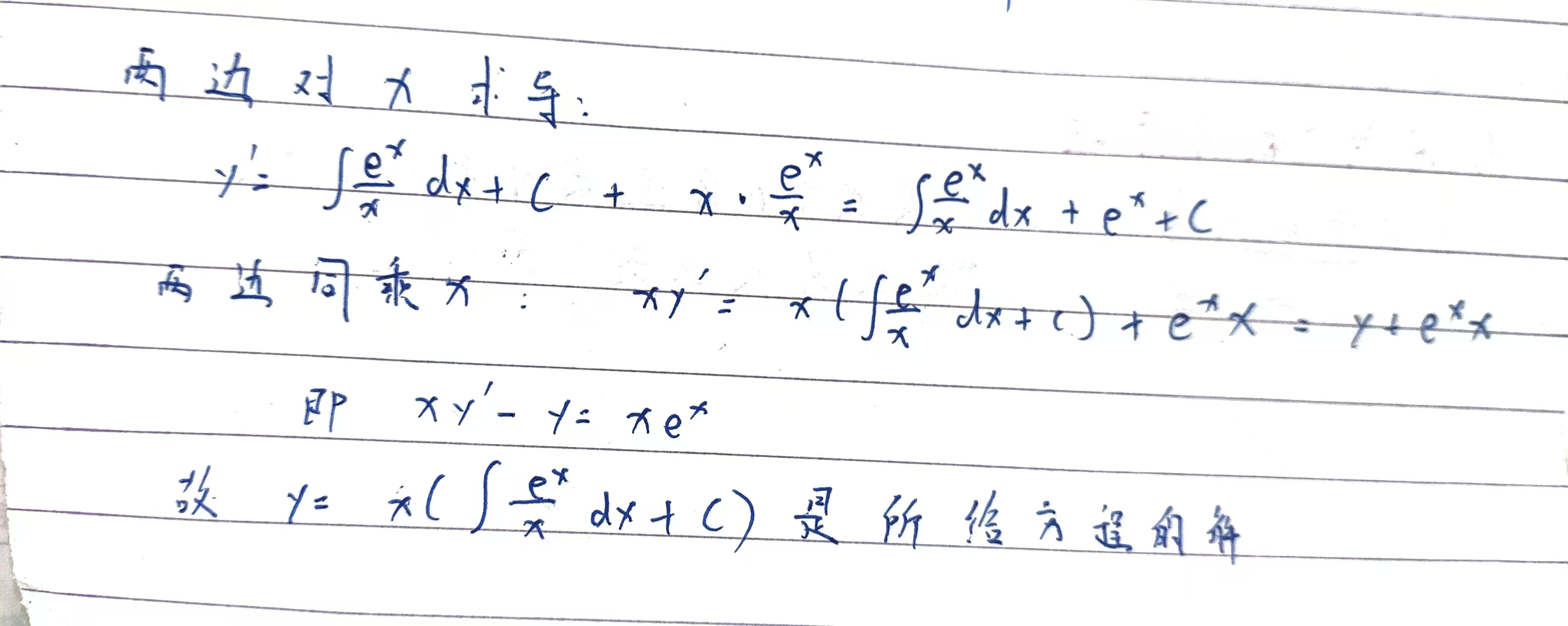
求初值问题的解
例题: 求以下初值问题的解: $$\begin{cases} y''' &= x \ y(0) &=a_0;,y'(0)=a_1;,y''(0)=a_2 \end{cases} $$

可分离变量的微分方程
基本概念

例题
求解变量可直接分离型微分方程
例题: 求解 $xyy' = (x+a)(y+b)$
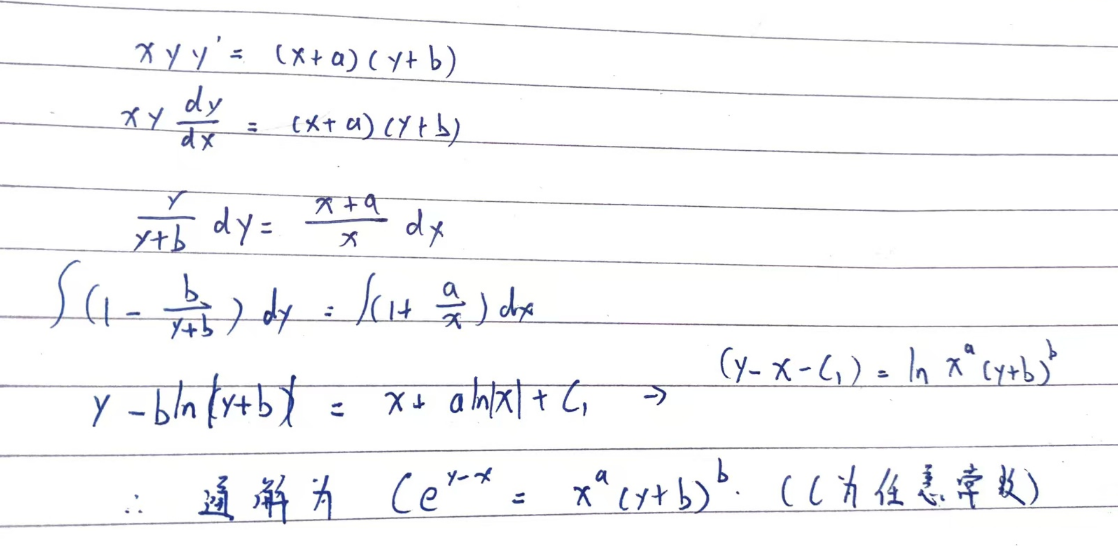
求初值问题的解
例题: 已知函数 $y=y(x)$ 在任意点 x 处的增量 $\Delta y = \frac{y\Delta x}{1+x^2}+\alpha$ ,且当$\Delta x \rightarrow 0$ 时, $\alpha$ 是 $\Delta x$ 的高阶无穷小 , $y(0) = \pi$ , 则 $y(1)$ 等于:
如果能够获得 $y(x)$ 的表达式 , 令 x=1 即可得到 y(1) 的值 , 由于 $\Delta y = \frac{y\Delta x}{1+x^2}+\alpha$ , 而 $\alpha = o(\Delta x)$ , 这说明 y 在 x处可微
函数可微的定义回顾
一个函数 $y = f(x)$ 在点 $x$ 处可微的定义是:存在一个常数 $A$(依赖于 $x$),使得当自变量增量 $\Delta x \to 0$ 时,函数增量 $\Delta y = f(x + \Delta x) - f(x)$ 满足: $$ \Delta y = A \Delta x + o(\Delta x), $$ 进一步,可以验证导数存在: $$ \frac{\Delta y}{\Delta x} = \frac{A \Delta x + \alpha}{\Delta x} = A + \frac{\alpha}{\Delta x}. $$ 取极限 $\Delta x \to 0$: $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \left( A + \frac{\alpha}{\Delta x} \right) = A + 0 = A, $$ 即
$$\frac{ dy}{ dx}=A=\frac{y}{1+x^2} $$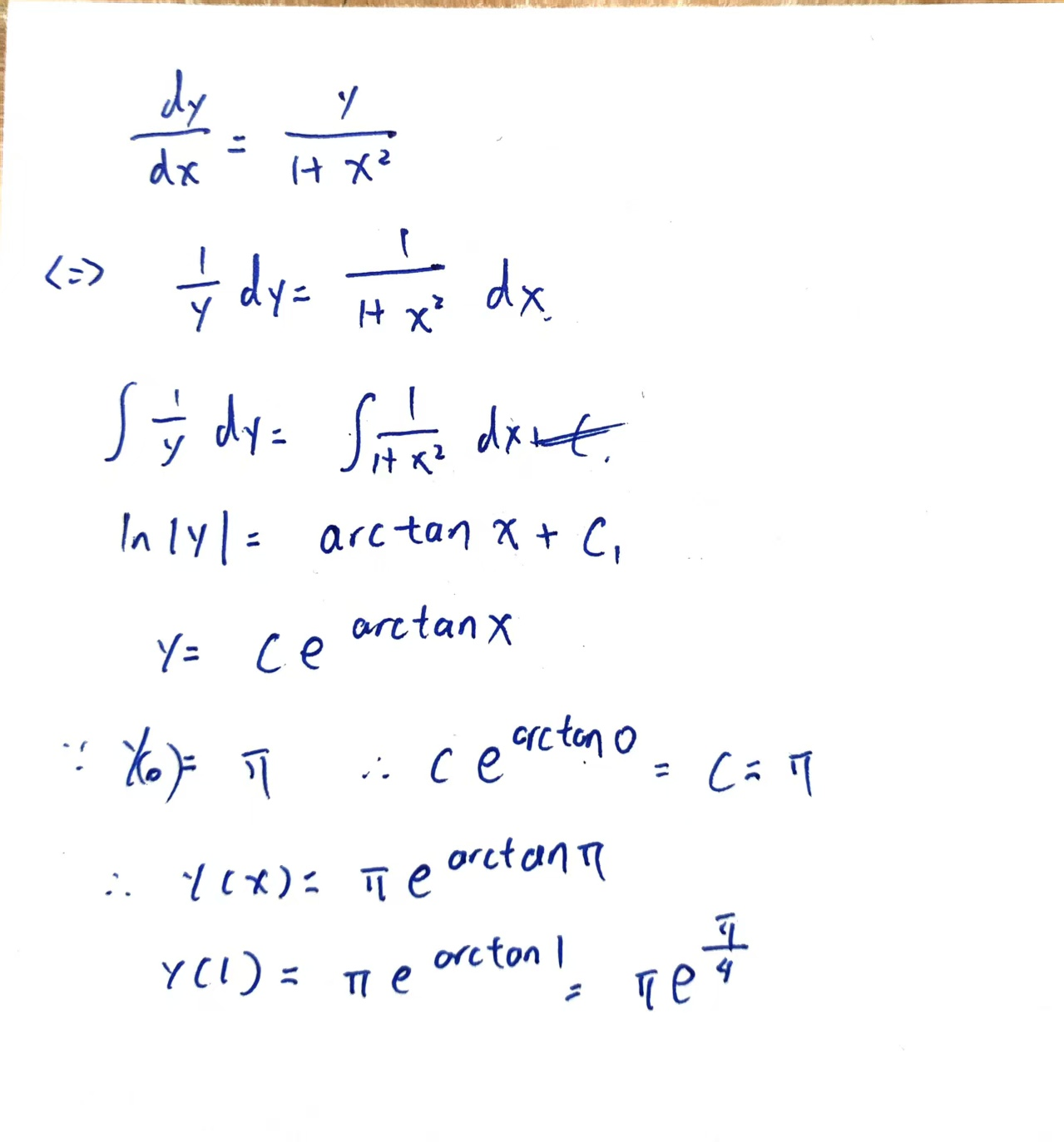
求解经变量代换可化为变量可分离型方程的微分方程
例题: 求方程 $x\frac{dy}{dx} +x +\sin(x+y) = 0$ 的通解.



此处评论已关闭